こんにちは、めたぼザビです。
2022年は利上げの年ですね!
今回は、そんなホットな金利と債券の関係について書いていきたいと思います。

なるべく基本のきから説明したいと思います!
金利とは
ここでいう金利とは、資金の貸し借りを行ったときに発生する対価全般を指します。
つまり、指す範囲が非常に広く、一見シンプルですが紛らわしい単語です。
主に以下のことを指すことが多いです。
利子、利息、利子率、政策金利
利子とは、お金を借りた際に、借りた金額(元本)以外に余分にやりとりする手数料のことです。
利息も基本的には同じ意味ですが、借手側が利子、貸手側が利息と表現することが多いです。
ただし、これは慣用的なものにすぎず、帳簿上の勘定科目では支払い側も支払「利息」を用います。

なんだ同じかよ。
利子率とは、利子の額を元本の額で割った数値を指します。利率ともいいます。
通常、1年あたりで表されることが多いです(年利)。
政策金利とは、民間の銀行が中央銀行(日本だと日銀)から資金調達する際の利率を指します。
最近、金利金利と世を騒がせているのは、米国の政策金利、FFレート(Federal Fund Rate)です。
これを決める会合をFOMC(Federal Open Market Committee)と呼びます。
利回り
利回りとは、言ってしまえば収益率、すなわち元本に対する収益の割合のことであり、受け手側の呼称です。
株式ではリターン、債券ではイールドと呼ばれることが多いです。

なぜ分けたし。
配当という、株式版利息のようなものが存在しますが、元本に対する配当の割合は「配当利回り」と呼ばれます。
利回りが利息と異なる点は、売却損益部分も含みうることにあります。
株式においては、配当+売却損益の割合となります(トータルリターン)。
債券においては、クーポン(利子)+売却損益の割合となります(YTM)。
YTMはYield to Maturityの略となります。
たいてい1年あたりのものを用いますが、文脈により各々判断していくことになります。
ここさえクリアしてしまえば、用語についてはややこしい部分は終わりです。

個人的に、債券のややこしいところは、このクーポン利子率と利回りが同時に出てくることにあります。
また、この利回りのことを単に利子率と呼ぶこともあり、これがさらにややこしくしてくれます。
債券とは
債券とは、資金調達の際に借り手側が発行する、「我々にお金を貸してくれたことを証明します」券です。
券面には、
・元本金額
・クーポンレート(毎年支払う利子率)
・償還期間(元本を返済するまでの期間)
が表示されています。償還とは、債券にかかる債務を返済することを意味します。
償還日までは利息を受け取り、元本は償還時に一気に受け取るタイプが一般的です。
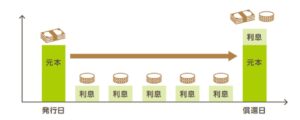
国が発行した債券を国債、会社が発行した債券を社債と呼びます。
クーポンレートがゼロであるものを割引債(ゼロ=クーポン債)と呼び、主に経済学の理論構築に用います。
通常は、クーポンレートがゼロではない利付債であり、レートが固定されている固定利付債と、固定されていない変動利付債に分かれます。
債券価格と利回りの関係について
前置きが長くなってしまいましたがいよいよ本題です。
ですがその前に、割引現在価値、というものを知っておく必要があります。
割引現在価値
いまの1円と、1年後の1円は、果たして同じ価値を持つでしょうか?
という疑問からスタートします。
いまの1円を利回り1%で運用した場合、1年後は、\(1\times(1+0.01)=1.01\)円である。
よって、今の1円と、1年後の1円は、価値が異なるといえます。
では、1年後の1円は、現時点でいくらなのでしょうか?
その金額を\(x\)円とおいてみると、上のように考えれば、
$$x\times(1+0.01)=1$$
が成り立つので、\(\displaystyle x=\frac{1}{1.01}\)円となります。
同様に考えると、2年後の1円は、\(\displaystyle \frac{1}{(1.01)^2}\)円となります。
わかりやすくゼロ=クーポン債で考える。
ここで、償還期間が5年、券面金額100円のゼロクーポン債を考えてみます。
利回りは\(r\)とします。
上記と同様に考えると、券面金額の現時点での価値は、\(\displaystyle \frac{100}{(1+r)^5}\)円となります。
この債券が市場で取引された場合、これより安くても高くても裁定取引(買うor売るで確定で利益が取れる状態)ができてしまうため、これが理論上の債券価格となります。
一般的に、分母の数値が大きくなると、分数全体の値は小さくなります。
つまり、利回りrが上昇すると、債券価格は下落するわけです。
クーポンがついても考え方は同じ。
ここで、上記のゼロクーポン債に、毎年10円のクーポンがつくとします。
このとき、1年後、2年後、3年後、4年後、5年後のクーポンの現在価値は、それぞれ
$${\frac{10}{1+r}}_{~~,~~}\frac{10}{(1+r)^2}_{~~,~~}\frac{10}{(1+r)^3}_{~~,~~}\frac{10}{(1+r)^4}_{~~,~~}\frac{10}{(1+r)^5}$$(横スクロールできます。)
円となります。
上記の元本の現在価値とこれらを足し合わせたものが理論上の債券価格になります。
式を見ると、いずれもrが上昇すると価格が下落するということがわかります。

おわかりいただけただろうか。。。
利回りと政策金利との関係について
債券について触れると、よく見かける単語に、イールドカーブというものがあります。
これは、横軸に〇年物債券、縦軸にその利回りをとったグラフのことを言います。
通常は、連続である(つながっている、くらいに思っておけばOK)ゆえにカーブを描きます。
横軸が左側に行くほど、政策金利に近い値になることが知られています(いわゆる短期金利)。
長期金利は、説明は割愛しますが、予想された短期金利の平均で表されます。
つまり、政策金利が直接債券価格に作用するのではなく、政策金利がまずYTMに影響し、それが債券価格に影響するという二段構えであることがわかります。
債券投資の分析に不可欠なグラフとなります。
分析の仕方については、専門書をご覧いただければと思います。
いろいろな債券の形
余談ですが、実は債券にはいろいろなオプションが付くことがあり、様々な形態をとります。
例えば、コーラブル債というものがありますが、これは、満期前に償還することができる借り手側の権利、が付与された債券になります。
反対に、プッタブル債というものがありますが、これは、満期前に償還をさせることができる貸し手側の権利、が付与された債券になります。
このように通常の債券にギミックが搭載された債券のことを仕組債とよびます。
まとめ
いかがでしたか?今回は債券の入門にあたる部分を、復習がてら説明させていただきました。
もし間違いや、読みづらいところがありましたらご指摘いただければと思います。
ご精読ありがとうございました!



コメント